
看不見的“遍歷性”
時間:20-03-30 來源:原創·老喻在加
看不見的“遍歷性”
如果沒有“遍歷性”,就會失去“概率權”。
這兩個與概率相關的概念結合在一起,告訴了我們在當下這個危機時刻最該做的兩件事:
1、別出局。
活著比什么都強。
要賺錢,你首先得活得長。
2、別旁觀。
不要浪費了你遭遇的危機。
參與其中,為未來下注,但不是簡單抄底。
上部分:別出局
一
我來邀你玩兒一個扔硬幣游戲:
假如你扔到正面,我給你100塊錢;
假如你扔到反面,你輸給我50塊。
你一看,這個游戲有利可圖,就接受了我的邀請。而且,你的運氣很好,扔到了正面,賺到了我的100塊。
請問:你參與這個游戲賺了多少錢?
慢,這不是廢話嗎?你心里想。你已經真金白銀地拿走了100塊,難道不就是賺了100塊嗎?
不對。
在我這種“概率主義者”看來,你只賺到了25塊。
為什么呢?分析如下:
a、當你扔出硬幣的時候,未來有兩種可能性,一種可能是正面,一種可能是反面。
b、我們用平行宇宙來打比方,那一刻,你的未來分叉為兩個宇宙:
在宇宙A里,“A你”賺了100塊;
在宇宙B里,“B你”虧了50塊。
c、我問這次交易你賺了多少錢,應該是“A你”和“B你”一共賺了多少。
d、所以,應該是100減50,然后兩個你對半分,是25塊。
你要對“別的平行宇宙里的你自己”負責任。
聰明如你一定會笑:
嘿,你是想教小朋友這么簡單的”期望值“計算嗎?
不,我要說的不是期望值,而是”遍歷性“。
二
遍歷(ergodic),字面的意思,就是“各態歷經”。
什么是”遍歷性“?
”遍歷性“是指統計結果在時間和空間上的統一性,表現為時間均值等于空間均值。
例如要得出一個城市A、B兩座公園哪一個更受歡迎,有兩種辦法:
第一種辦法。在一定的時間段考察兩個公園(在空間上考察)的人數,人數多的為更受歡迎公園;
第二種辦法。隨機選擇一名市民,跟蹤足夠長的時間(在時間上考察)來統計他去兩個公園的次數,去得多的為更受歡迎公園。
如果這個兩個結果始終一致,則表現為遍歷性。
這個概念最早來自統計力學。
統計力學運用的是經典力學和量子力學的原理。
一個粒子運動,可以按照牛頓力學方法,計算它的運動速度、軌跡等。
但如果是大量的粒子,就很難計算,只能用統計方法計算,即概率論的方法計算。
物理學家玻爾茲曼和吉布斯假設一個密閉容器,里面有氣體分子在運動,他們不斷的相互碰撞,并和容器壁碰撞,每碰撞一次,它們的運動狀態就改變一次。
如果氣體分子足夠多,碰撞的時間足夠長,那么這個密閉容器中的每一點都會被氣體分子經過。
如果你是個打過桌球的男生,一定有過這樣的怪念頭:
假如球可以無限運動下去,一定可以進洞。
于是你就使勁地胡亂捅了一桿,結果......你的白球進洞了。
回到科學。一個單獨的氣體分子,隨著時間的流逝,也會造訪容器中的每一點,物理學家們就可以通過使用一群氣體分子的平均特性,來預測單個氣體分子的特性了。
所以,遍歷性的學術性解釋是統計結果在時間和空間上的統一性,表現為時間均值等于空間均值。
三
”遍歷性“在塔勒布的哲學世界里,是個核心詞匯。
對于這個很難解釋的詞匯,他舉了個例子。
(以下摘自《非對稱風險》一書)
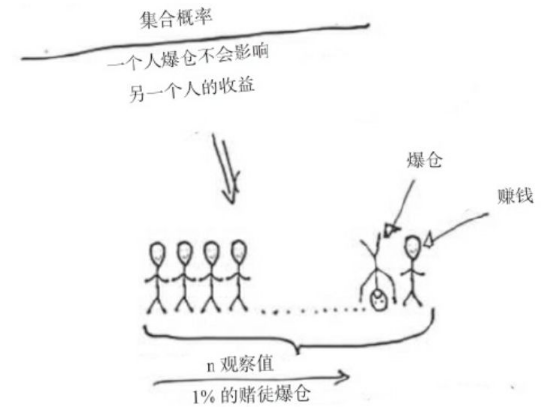
第一種情況:100個人帶著總共100萬去賭場玩兒24小時。他們有的人賠錢,有的人賺錢。
我們計算一下回來的人口袋里剩下的錢,就可以計算出他們的總體收益,進而計算出賭場對賠率的定價是否合理。
假設一天玩下來,第28號賭徒爆倉(賠光)了,第29號賭徒會受到影響嗎?
不會。
比方說,你根據這個樣本可以很容易地計算出其中大約有1%的賭徒會爆倉,如果一直重復這個過程,你會得到與之前相同的比值,即在同一時間段內,平均有1%的賭徒爆倉。
這個叫集合概率。一個人爆倉不會影響另一個人的收益,總體看來全體賭徒的輸贏與賭場的賠率一致。
我們可以這么想,這100個人是并聯關系,每個人的行為是并行的,掛掉一個,不影響另外99個繼續前行。
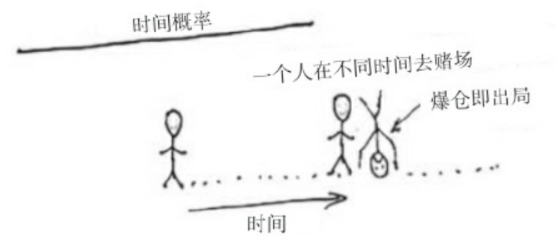
第二種情況:你表弟帶著總共100萬,去賭場玩兒100天。
在第28天的時候,你的表弟不幸爆倉了,那么對于他而言,還會有第29天嗎?
不會有了,因為他觸發了自己的“爆倉點”,在游戲中他已經永久地出局了。
這個叫時間概率。
我們又可以這么想,這100個人是串聯關系,每個人的行為是串在一起的,掛掉一個,整條線就斷了。
塔勒布對此解釋道:
100個賭徒在1天時間里的成功概率,并不適用于你表弟在100天時間里的賭運。
第一種情形稱為集合概率,第二種情形稱為時間概率;
第一種情形涉及的是一群人,第二種情形則涉及一個人穿越一系列時間。
由此,塔勒布給出定義:
如果有一個隨機過程,其過往的歷史概率不能適用于其未來的情景,那么這個隨機過程就不具有遍歷性。
出現上述情況是因為系統存在一個類似于“叫停”的機制。意思就是出局了。
一旦出局,你就不能回到隨機過程中繼續游戲了。由于不存在任何可逆性,我們稱之為“爆倉”。
這里的核心問題是一旦存在“爆倉”的可能性,那么成本收益分析就變得毫無意義了。
好玩兒的是,這個詞語的背后是概率,而概率的概念最早來自賭場。所以最好的和概率有關的例子大多和賭場有關。
更直接一點兒的例子就是俄羅斯輪盤賭游戲:
左輪手槍里只放一個子彈,大家輪流對自己開一槍,每玩兒一輪,至少掛掉一個,然后大家分掉這個倒霉鬼的錢。
表面看起來是有5/6的概率賺到錢,算是大概率吧。
但是如果你無法承受小概率的失敗,再大概率的成功也沒有意義。
在俄羅斯輪盤賭游戲中,掛掉的那個人,他的爆倉對于他本人而言不是遍歷性的。
由于他爆倉出局,導致無法實現時間概率的遍歷性。
但對于系統而言是遍歷性的。
對于系統而言,有人爆倉出局體現了集合概率的遍歷性,所有可能發生的早晚都會發生。
有人會說,現實中誰會去參加俄羅斯輪盤賭游戲呢?
在我看來,那些有莊家控制的投機游戲,連俄羅斯輪盤都不如。
你自己想想我說的是什么吧。
以上種種告訴我們,預防系統因遍歷性而產生的極端情況,應該成為我們首要關注的事物:
要防止自己成為系統遍歷性的犧牲品。
四
我是今天才翻了一下塔勒布的《非對稱風險》。
假如他知道我創造的“概率權”這個詞,一定會很喜歡。
塔勒布在該書語境中所說的遍歷性,是指對一群人在同一時間的統計特性(尤其是期望) 和一個人在其全部時間的統計特性一致,集合概率接近于時間概率。
我所創造的“概率權”,是指概率是一個人的權利。人們對這項權利的理解和運用,決定了現實世界中財富的分配。
如果沒有遍歷性,那么觀測到的統計特性就不能應用于某一個交易策略,如果應用的話,就會觸發“爆倉”風險(系統內存在著“吸收壁”或“爆倉點”)。
換句話說,如果沒有遍歷性,統計特性(也就是概率,以及對應的“概率權”)不可持續。
遍歷性和概率權,這兩個與概率相關的概念結合在一起,告訴了我們在當下這個危機時刻最該做的兩件事:
1、別出局。
活著比什么都強。
要賺錢,你首先得活得長。
2、別旁觀。
不要浪費了危機。
參與其中,但不是簡單抄底。
五
我們正在經歷一場從未遇見過的危機。
無人能夠置身事外。
盡管“準確”預測并且“神勇”做空,達利歐的橋水還是在微信群里“被爆倉”了。
達利歐的確爆過倉。那是在1982年,他極其準確地預測到墨西哥債務違約,并買入黃金和國債期貨。
但是沒想到在美聯儲的刺激下,股市反而開始了一場大牛市,達利歐賠得精光。
原因有二:
1、他預測到了結果,但沒預測到結果的結果;
2、他使用了錯誤的下注方式,要么全贏,要么全輸。
年輕時候的達利歐意氣風發,然而,那時的他不懂什么叫“遍歷性”。
2016年,物理學家奧利.彼得斯和諾貝爾物理學獎得主默里.蓋爾曼寫了一篇關于遍歷性的論文,里面有個例子:
有個玩硬幣的賭博游戲,你投入1元,50%可以得到0.6元,50%可以得到1.5元。
根據期望值計算,一半可能性損失40%,一半可能性盈利50%,算下來數學期望是5%。
用流行的話說,這是大概率賺錢的事情,你可以大膽玩這個游戲。
不過,這個游戲有兩種玩兒法,確切說,是有兩種不同的下注方式:
方式a:你每次都拿1塊錢去玩,假設你有無限多個1塊錢,你可以一直玩下去,從長期來看你肯定是賺錢的,平均每把用5%的數學期望算是0.05元。
缺點是太慢,而且你必須有足夠多的時間能玩下去。
方式b:拿出自己能拿出的最大的資金,然后投入進去。
后面這種玩兒法,就是所謂的All in。看起來極端,其實很多人都是這么干的,我自己也經歷過,誰沒年輕(蠢)過啊。
我們來做個簡單的計算吧。
你本金一百萬,第一把贏,第二把輸,第三把再贏,如此持續下去。
直覺上看,100萬本金,贏了是賺50萬,輸了是虧40萬,為什么不能玩兒呢?
拿張紙,用中國當前幼兒園小班的數學能力計算一下:
100萬??(1+50%)??(1-40%)??(1+50%)(1-40%)......
一直這么玩兒下去,你會發現,沒有幾把就沒錢了。
這難道不是絕大多數普通人做投資的現實嗎?
對比左輪手槍的例子,這個關于“遍歷性”的解釋,更像一把慢刀子。
韭菜自己被割起來更加無痛,沒準兒還覺得是自己被割的時候姿勢沒擺好,天天繼續勤學苦練,把辛辛苦苦的錢接著拿去All in下一個風口。
萬維鋼講過一本叫《一個數學家玩轉股票市場》的書,作者約翰·保羅士是一位數學家。
估計數學好的聰明人都曾幻想過在股市里搞一搞,保羅士在股市上賠了很多錢,有切膚之痛,于是寫了這本書。
書中有道和前面寫到的蓋爾曼的題目類似的數學題。
這類簡單的題實在是太迷惑人了,所以我不厭其煩地再來一次:
假設任何一只股票 IPO 第一周,一半可能性上漲80%,一半可能性下跌60%,
現在,我們搞個投資策略,每周一買一只 IPO 的股票 ,周五把它賣了。然后不斷重復。
假設我們有1萬本金,請問年底能賺到多少錢?
這里有兩種計算方式。
計算方式1:簡單地根據期望值計算
每周的投資回報期望值是:
(80%-60%)??50%=10%
每周賺10%,一年下來利滾利,就是1.1的52次方。
如果我投入了1萬元,到年底我會有142萬元。
真是這樣嗎?不是。
計算方式2:殘酷的現實
你實際的回報,應該是:
1萬??(1+80%)??(1-60%)??(1+80%)(1-60%)......
52周下來,你還剩下1.95元。
盡管這個計算非常簡單,但絕大多數人其實都想不明白。
142萬和一塊九毛五,到底哪個計算是對的?
都對。
142萬元,就是市場的平均回報。
1.95元,是你的這種策略的回報。
你的這個系統沒有遍歷性。
一群人做一件事取得的平均值,和一個人經歷這件事很多很多次,是不一樣的。
那該怎么辦呢?模仿指數基金,購買所有IPO的股票,這樣,你就能夠實現“遍歷性”,得到142倍的回報。
這就是為什么巴菲特說普通人應該去買指數基金的原因。
(在這里埋下一個蛋給聰明家伙:如果所有的人都按照指數法,也就是上面的計算方式1,那是不是所有的人都賺了142萬,那誰虧錢了?又如果所有的人都按照上面的計算方式2來買,所有的人都虧到只剩下1塊多錢,那么誰賺錢了?)
遠在1982年,哈佛畢業的達利歐在賠光褲衩之后,終于意識到:
通過市場交易賺錢十分困難。
靠水晶球(預測)謀生的人注定要吃碎在地上的玻璃。
哪怕你的預測大概率正確,你也會因為沒有“遍歷性”,而一敗涂地。
隨后,達利歐重新尋找“投資的圣杯”,橋水東山再起。他的秘密是:
如果擁有15-20個良好的、互不相關的回報流,就能大大降低風險。
簡而言之,就是既避免爆倉的風險,又盡量賺得多一些。
2008年,幾乎所有人都虧得一塌糊涂,橋水還能賺14%。
2019年11月,橋水基金通過衍生品市場投入15億美元押注全球股市在未來三個月下跌。
然而,這只占他們1500億美元基金規模的1%。
2020年,一場病毒席卷全球。橋水建立了140億美元空頭頭寸,押注歐洲公司股票因新冠疫情惡化而持續暴跌。
盡管如此,橋水的旗艦基金今年(現在是3月)已經虧了20%。
這一次,全球很難“互不相關”。
但是,可以預測,橋水一定是投資機構里比較好過的那一批。
我看到有人說,假如這次橋水真的爆倉了,那《原則》這本書就白看了。
其實多慮了,說得好像他曾經看懂了那本書似的。
六
遍歷性告訴我們,要想著那些看起來并沒有發生的平行宇宙里的“我”。
簡單點兒說,我們別太羨慕那些現實中的“贏家”。
比方說,某個靠炒幣身價過10億的人,在“遍歷性”的平行宇宙的某個空間,某個“他”因為虧光而走投無路;
又好像某個首富,名利雙收風光無限,但是在某層“遍歷性”的平行宇宙里,他正遭受牢獄之災。
很多所謂的贏家,只是幸運的傻子,算上那些替他受罪的另外一個概率時空的“他”,他其實是個輸家。
《隨機漫步的傻瓜》建議不以結果論英雄,而是從“假如歷史以另一種方式呈現”出發論斷成敗。
你也許會說,這個世界不是以成敗論英雄嗎?
請記住,我們的一生,最終是統計的結果。
“歷史存在著多種可能,我們不能被歷史的一小段過程所迷惑,而要在較大尺度的歷史范圍內考察一切。”
從“遍歷性”去計算,正是《對賭》里所說的,不能簡單從單局的結果來評估決策判斷的質量。
重點在于:
思考帶來決策,決策產生行為,行為養成習慣,習慣塑造個人決策系統,個人決策系統決定命運。
再往前一步,“遍歷性”警告我們,你的幾百幾千個平行宇宙中某個看起來似乎毫不起眼的“你”,一旦炸掉,有可能讓你所有的平行宇宙同時坍塌,無一幸免。
要小心那些造成不可逆傷害的、系統性的風險。
這些風險,通常看起來都是極小概率的、百年不遇的。
然而,“遍歷性”告訴我們,那些看起來似乎極難發生的小概率災難,也許早晚都會發生。
也就是說,某個時間下極小概率的事件,會隨著時間疊加起來。
請看題目。
幸存的青花瓷
明青花瓷非常值錢。例如,明永樂年間的青花如意垂肩折枝花果紋梅瓶(高36.5 cm),2011年曾以1.6866億港元成交。
我們假設一只青花盤在一年內被失手打破的概率是3%。
如果明朝正德年間(距今約500年)生產了一萬只青花麒麟盤,請問現在還有多大可能性見到這種盤子?
(題目來自何書元編著的《概率論》)
假如不計算,你隨便估一下,現存多少正德青花麒麟盤?
記下你估算的數字,接下來看答案。
計算方法如下:
第一步,先計算一只青花盤流傳至今不被打破的概率。
500年間不被打破的概率p=(1-0.03)的500次方=2.43乘以10的負七次方。
所以,被打破的概率q=1-p=0.999999756
第二步,計算一萬只青花盤流傳至今不被打破的概率。
一萬只青花盤全被打破的概率是q的一萬次方=0.99757,
那么這一萬只盤子,至今仍有幸存的概率是1-0.99757=0.00243。
也就是說,在今天,有千分之2.43的概率還能見到這種青花盤。
在這個非常簡單的計算中,即使是聰明的人也會有個錯覺:
每年打碎的概率是3%。如果今年沒打碎,那么明年開始打碎的概率還應該是3%呀,這難道不是獨立事件嗎?
錯誤在于,我們需要的是n年不打碎的概率,所以就要用(1-3%),然后不斷相乘。
97%乘下去,乘不了多少次,就衰減成一個很小的概率。
時間作為驚人的變量,令青花盤被打碎的這個小概率事件,成為“歲月遍歷性”里的大概率事件。
你的腦海中會不會浮現出一句話:
該碎的東西,早晚會碎。
這不就是墨菲定律嗎?
墨菲定律是指:“凡是可能出錯的事就一定會出錯”。
讓墨菲定律成立的前提有兩個:
1、大于零的概率;
2、時間夠長(即樣本夠大,不管是時間還是空間)。
我稱之為“概率的時間復利”。
(這種基于概率的時間疊加,非常違背人的直覺。我會單獨寫一次這個主題。)
墨菲定律似乎是熱力學第二定律的世俗版。
遍歷性和墨菲定律,相會于熱力學的復雜世界。
塔勒布警告我們:對于那些極小概率的致命傷害,要有杞人憂天似的偏執。
警惕極小概率的肥尾風險。
我隨便列個不全清單吧:
賺錢時悠著點兒;
別太追求所謂極致;
別賭;
遠離爛人;
別黃賭毒;
系上安全帶;
戒煙戒酒;
交幾個危難時刻能夠把你藏起來的朋友;
住酒店時看一下逃生路線。
英國軍人瑞克,退役后做安保工作,任摩根士丹利安全副總裁,在世貿中心的南塔上班。
瑞克近乎偏執地認為,世貿中心早晚會受到攻擊,他一方面要求公司搬走,一方面強硬地讓所有員工參加逃生訓練,每年2次,哪怕是大老板,哪怕是交易時間,2人1組下樓梯,直到第44層。他用秒表計時,懲罰那些行動遲緩的員工,確保緊急狀態下員工都能迅速行動。
如你所知,電影都想像不到的極小概率事件發生了,2001年,兩架飛機分別撞上了世貿中心。在兩次撞擊間隔的15分鐘里,摩根的2687名員工,連同正在摩根談業務的250多名股票經紀人,安全地撤到了44層。
據說,指揮撤退的瑞克為了安撫騷亂的人群,唱起了一首叫《哈里克的男人》的歌:
康沃爾的男人穩穩地站著。
戰斗的英雄永遠不會沒有準備。
站著永不屈服。
……
已經安全撤離的瑞克,像船長一樣又掉頭上樓,再沒回來。
下圖是他給妻子的遺言,和人們紀念他的雕像。

這和塔勒布奉行生存第一的理性法則并不矛盾。瑞克最大限度地救下了最多的人,并不惜犧牲自己。
所謂理性就是首先保證自己所在的集體生存更長時間。
瑞克不僅先知般預測了風險,而且堅定地防范了風險,最終勇敢地承擔了風險。
這可能是人類理性當中最不可言喻的偉大之處。
下部分:別旁觀
七
首富巴菲特的背后,也是“遍歷性”。
假如我們只看見“別人樂觀的時候我悲觀、別人悲觀的時候我樂觀”,那就太簡單了。
那么簡單,為什么我們總學不會?
真的只是因為每個人都不愿意慢慢變富嗎?
當然不是。
2020年的這場危機,如果說巴菲特預測對了,似乎有點兒勉強。
今年(2020年)2月22日,巴菲特在致股東的信里說:
在給出這一樂觀預測的同時,我們也要發出一項警告:未來股價可能會發生任何變化。有時,股市會暴跌,幅度可能是50%,也可能會更大。
有人說股神抄底被套,增持達美航空4500萬美元,增持紐約梅隆銀行3.59億美元,增持后股價暴跌。
這點兒算啥呀,巴老截至2019年末持倉的股票市值高達2480億美元,大多成本較低。
同時,他手握現金超過1250億美元。
又到了他拿著臉盆滿地撿錢的時刻。
巴菲特不喜歡預測宏觀,但不代表他對宏觀沒有預測。
他有一個很喜歡的市場指標:股票總市值與GDP的比值。
在2000年互聯網泡沫高峰時期,美股與美國GDP的比值高達146%:
在2008年金融危機爆發前為137%:
在2018年,這一數字為148.5%。
過去兩年,巴老一邊重倉蘋果公司,一邊大舉囤積現金。
在危機時刻,既能做到不爆倉,又能抓住機會大賺一筆,等于要同時做好兩件事情,就像用一只箭射下兩只飛鳥。
我們還是要說回遍歷性。
巴菲特有一句至理名言:“ 要賺錢,你首先得活得長。”
這只是其一,對應的是本文的上部分:別出局。
一直喜歡索羅斯而踩巴菲特的塔勒布,對此評價道:
他的成功從來都不是依靠復雜的成本收益分析賺來的,恰恰相反,巴菲特只是建立了一個非常嚴格的篩選體系,只有通過篩選的項目他才進行投資。他曾經說過,成功人士和真正的成功人士之間的區別就是后者幾乎對所有投資機會說“不”。
塔勒布說自己的觀點與巴菲特類似:
對尾部風險說“不”。
許多方法都可以賺錢,且完全不必觸發尾部風險。
許多方法可以拯救世界,完全不必使用那種會導致系統脆弱性和未知風險的復雜方法。
然而,“說不”的目的,是為了機會來臨的時候可以大舉進攻。
別掛掉,這樣你才有機會保護“遍歷性”;
要出手,這樣你才有機會實現“遍歷性”。
不因“遍歷性”而死,亦不要錯失“遍歷性”的指數型回報。
不從你遭遇的危機中獲利,在恐慌中躲在角落,即使沒有爆倉,其實也是隱性出局。
下面要說的,對應的是本文的下部分:別旁觀。
八
巴菲特在眾人悲觀時出手,以實現“遍歷性”,以及撿到那些被放棄的概率權,靠的是什么?
首先,不是準確預測,也不是精確抄底。
巴菲特不喜歡預測宏觀,也不擅長于抄底。
巴菲特的師傅格雷厄姆因為抄底曾經死得很慘。
歷史上好幾次巴菲特大舉買入后,股價繼續下跌,而且還跌得很多。
這是他堅守“價值投資”之道的原因。
把股票當作公司所有權的一部分,假如股票下跌,相當于自己想要的東西打折甩賣,何樂而不為?
同時,他也會鬼精地設計各種安全抄底,例如買可轉換優先股。

當然,看錯了公司是另外一回事。那就認錯,賣掉。
實現遍歷性,需要源源不斷的彈藥,以及聰明的下注方式。
巴菲特的公司,總部只有25人,卻管理了市值數千億美金的很多家公司。
他放權管理,只要求一點:公司把賺到的錢源源不斷地交上來。
巴菲特選擇好公司的標準,其中有一條就是資本支出小自由現金流大。
外加保險公司的浮存金,巴菲特擁有泉水般的資金彈藥。
加上價值投資的護城河,以及堅決不加杠桿的自律,在股市這個“遍歷性”游戲場,巴菲特可以一直下注。
巴菲特的資金量很大,所以逆勢建倉是機會,左側買入是常態。
長期持有是另外一種下注方式。你可以理解:長期持有是每天賣掉手上持有的股票,然后繼續再買回這些股票,然后一分錢交易費用都沒有。
此外,巴菲特的資金幾乎沒有什么時間期限,都是十年以上的長期浮存金或者永續資本。
當然,還有索普研究出來的關于下注的凱利公式。
時間是“遍歷性”的朋友。
這里的時間,包括時間的長期性,以及周期的波動性。
九
馬克斯在《周期》中文版序言中說:
如果我們能夠正確地理解周期、判斷周期和利用周期,在周期的每個重要轉折點采取相應的投資行為,就能長期戰勝市場。
周期的特點是,市場要么過于悲觀,要么過于樂觀。
就像叔本華說的:
人生就是一團欲望。當欲望得不到滿足便痛苦,當欲望得到滿足便無聊,人生就像鐘擺一樣在痛苦與無聊之間擺蕩。
難題在于,你永遠無法知道,現在股市是處在過于悲觀的階段,還是過于樂觀的階段。
我贊成不去精確預測周期,但是要理解周期。
真正“靠預測賺錢”的鼻祖,是西方思想史上第一個有記載留下名字的思想家,被后人稱為“科學和哲學之祖”的泰勒斯。
泰勒斯曾被人嘲諷“哲學是一項無用的事業”,于是他憑借自己的天文學知識早在冬天就預測到了來年的橄欖大豐收,因此他以微小的成本在米利都和開俄斯島租賃了榨油坊。由于無人競爭,他成功在來年通過出租榨油坊獲得了大量利潤。
亞里士多德記載了這個故事,并且說:
“只要哲學家們愿意,他們很容易致富;只不過這并不是他們的追求。”
然而,塔勒布認為,泰勒斯的發財,靠的不是天文學的預測,而是基于概率和期權的下注。
重點在于泰勒斯能用“一小筆錢”獲得租下大量的油壓機的權利,這被認為是歷史上有記載的最早的“期權”案例。
泰勒斯的賺大錢秘密,靠的不是準確預測天氣,而是自己創造了一個“凸性機會”,如下圖:
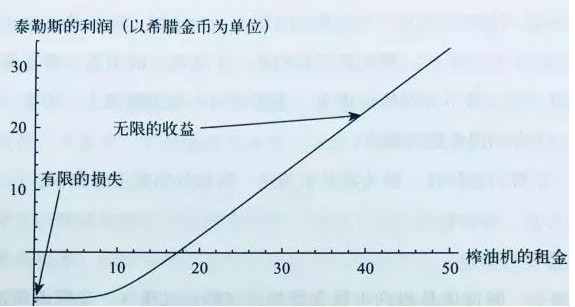
我在《如何用小概率賺大錢?(更正版)》一文中詳細講述過這個話題。
這其實是一次逆向應用黑天鵝的精彩案例。
“遍歷性”下的黑天鵝,大多時候是反向的,也有時候是正向的。
讓我們再回到“預測”這件事兒。
除了算命先生,極少有人能靠精確預測來賺錢。
即使你可以極為準確地預測一件事會發生,你也很難預測這件事情究竟何時發生。
這就像是要把幾個鵝卵石疊起來,難度太大了。
即使是達利歐、巴菲特等大神,也做不到。
更何況,現實世界的發展是非線性和不對稱的,“百年不遇”的事情隨時都可能發生,巴菲特89年見過一次的熔斷在一周內就發生了好幾次。
所以塔勒布說,黑天鵝事件無法預測。
你唯一可以做的,是讓自己不要被黑天鵝殺死。
(厲害的話還能去抓只肥天鵝。)
我們只有像沖浪運動員那樣,享受波峰和波谷,在“遍歷性”中生存,強大。
十
一旦拿來做類比,多精確的概念都會有模糊之處。在塔勒布的書中如此,在我的文中也是。
塔勒布在書后列了一大堆數學公式以及技術性附錄,用于維護自己的“學術權威”。
完全遍歷性的反面,是一種吸收態。
吸收態,是指當粒子撞上一個吸收壁,它們會被吸收或黏住。
吸收壁就像是一個陷阱,一旦被吸收進去就出不來。
比方說財富,有錢的人更容易賺到錢,而沒錢的人更難賺到錢。
又比如說,牙醫領域是個“吸收態”較弱,“遍歷性”較強的行業,大家的收入比較均勻。
很多行業的所謂“紅利”,都被寡頭獨吞了。例如智能手機。與其擠進去,不如做智能手機生態鏈的事情,包括硬件、軟件和服務。
例如羅永浩放棄智能手機而做直播帶貨,目前看起來是個聰明的選擇。
他仍然身處智能手機掀起的超級浪潮之中,并未真正出局。
但是對比起做手機,“直播”有更好的“遍歷性”,也契合他的基因。祝他好運。
我們還可以說,一棵有“遍歷性”的果樹的價值是小樹苗價值的很多倍。褚時健能做成褚橙,是因為他本來就是一個像種樹那樣來經營企業的人。
前陣子韓國圍棋世界冠軍崔哲瀚九段兼職當撲克牌選手,他自己的說法是棋賽太少,時間充裕,所以開始新挑戰。
但在我看來,是因為圍棋領域的獎金主要都被最厲害的幾個棋手瓜分了,而德撲呢,隨機性更強,更有“遍歷性”。
所以,從另外一個角度看,對于競爭環境的選擇,也就是說到底選擇哪個行業,哪個領域,“遍歷性”也是一個有趣的思考工具。
最后
該說的都說了,但是為了票房,還是要總結幾個干貨。
“遍歷性”對個人而言,有什么用呢?
下面給出十個建議:
建議1:你要對“別的平行宇宙里的你自己”負責任。
這其實是對未來的你負責任。
有些看起來極小的集合概率,會通過時間疊加起來,形成要命的墨菲效應。
建議2:把自己的一生當作一盤棋來下。
人的一輩子就是一個蒙特卡羅發生器(我忍住沒展開寫這個),是一個概率統計的過程。
長久的行為方式,遠比暫時的結果更加重要。
建議3:警惕那些極小概率的風險,不管利益有多大。
假如失敗的結果無法承擔,多高的期望值都不值得去下注。坐飛機呢?約百萬分之一的風險,可略。
不要有僥幸心理。
建議4:別出局,保護自己人生的“遍歷性”。
只要活得久,一切都可能發生。
做對的事兒,知錯就改,別賭,別情緒崩潰。
建議5:別旁觀,為自己的“遍歷性”持續下注。
不好的季節,往往是耕種的好時候。
在大家都慌張的時候,看看能夠埋下什么種子。
例如開始慢慢用閑錢定投指數基金,或者悄悄開個抖音號。
建議6:像沖浪那樣平等享受波峰和波谷,享受整個旅程。
這方面我們要向植物學習,一年四季,花開花落。
苦中作樂,是一種理智的選擇。
建議7:別試圖預測未來,而是提高自己的生命力。
生命力就是“反脆弱性”,就是在不可測的環境中茁壯成長。
測試一下自己對現有生存條件的依賴性,例如是不是離開現在的工作就活不下去,離開了某個人生活就會崩潰。
2020年的這場危機,測試了很多行業,很多公司。
人們開始重新理解“在線”的價值。你該如何參與其中?
建議8:主動設計自己的“遍歷性”。
假如你是頂尖厲害的人,選擇那些“分布不勻”的吸收態行業,例如基金經理,明星;
假如你是喜歡平平常常的人,選擇那些平均收益較高的“遍歷性”的行業,例如醫生,老師,工程師。
建議9:構建護城河,留有冗余。
別總處在絕境。總在為下一頓操心的人無法做出正確的選擇。
吃飽后,試著去做一些吃飽了撐著的事情。
建議10:守住大錢,虧點兒小錢。
不要拿自己輸不起的錢去冒險。
主動投資一些小錢,在那些肥尾的小概率事件上,敢于積極試錯。當然,要是那種正期望值的事情,而非買彩票買幣。
我們這個時代最奇妙的地方是:幾乎每個十年都是完全不同的。
上世紀的70年代、80年代、90年代,恍若隔世。
這個世紀的第1個十年,第2個十年,第3個十年,各個不同。
不確定性,是這個世界的常態。
我們過去這三十年一路向上的好時光,才是“意外”的、奇怪的小概率事情。
當然,更奇怪的事情,是:
太陽何以如此牢靠地、接近于100%地升起?
水和空氣為什么能恰到好處地供養我們?
大氣層如何這般脆弱而又盡職地包裹著我們?
如此種種。
假如真有造物主,祂已經在我們生存所依賴的99%的事物上,提供了接近于100%的大概率。
而類似于病毒、環境污染、核戰爭等極小概率的威脅,也許是廣義進化論的一部分。我們必須有所準備,不被其殺死。
除此之外,生活中絕大多數困擾我們的小概率,其實都是人類百無聊賴的產物。
別為了那些可要可不要的小概率的浮世誘惑,而失去我們極大概率擁有、且不能承受其失去的陽光和雨露。
照顧好自己,活久點兒,我們會“遍歷”更多百年不遇、千年不遇的未知。
摘自—原創·老喻在加
| 上一篇 | 下一篇 |
|---|---|
| 朱民:我曾經歷過多次危機,但目前的情況是最... | 同為全球PE巨頭,KKR在房地產領域投資為啥不如... |

